AI is a rapidly advancing field, with new papers detailing novel neural network architectures and diverse problem-solving approaches emerging almost daily. However, breakthroughs are less frequent; the field more often progresses through incremental changes.
This is especially true for the domain of explainable AI. Most AI research focuses primarily on making models more efficient at solving specific tasks. After all, a model by itself is useless if it doesn't effectively help us in solving a particular problem. While it is logical to prioritize enhancing models' task-solving capabilities, this emphasis often leads to the relative neglect of explainable AI, at least in comparison.
Kolmogorov-Arnold Networks, at first glance, appear potentially superior to the models we already have and not only. They also enable us to dive deeper into the inner workings of AI models. This helps us better understand what is happening "under the hood" of an advanced artificial neural network.
What Is Explainable AI
Artificial neural networks are classified as black box models due to their complexity. This makes it exceptionally difficult to decipher their decision-making processes. This is especially true for more sophisticated models, such as the ones based on the Transformers architecture. Indeed, these models are known for their remarkable predictive power and accuracy, however, this comes with a downside. They often contain millions or even billions of parameters, making it virtually impossible to trace the model's "thought process."
This characteristic of AI models is far from ideal. However, many are willing to overlook the inability to precisely determine how these models make their predictions as long as they produce good results Yet, in sensitive fields such as healthcare, finance, legal systems, and similar areas, the opacity of black box models like neural networks becomes a significant barrier to successful application. In these fields, even minor errors can have drastic consequences, potentially impacting people's lives, or in extreme cases, costing lives. Therefore, without achieving a certain level of interpretability, resistance will persist from those who believe that the lack of accountability in these situations is unacceptable.
Research on the explainability of AI models, while not as extensive as the research focusing on improving model performance, is still a significant and growing field. Explainability in AI is usually approached using two main types of techniques:
- model-specific methods
- model-agnostic methods
Model-specific methods are designed to explain the behavior of a specific type of model. For example, techniques like DeepLIFT, Grad-CAM, and Integrated Gradients are used for interpreting deep learning models, while decision trees can be visualized to show the decision-making process from top to bottom. These methods are tailored to particular models and provide insights that are unique to those models.
On the other hand, model-agnostic methods, such as LIME and SHAP, aim to explain the predictions of any machine learning model without depending on the model's internal workings. These methods can be applied across different types of models, offering more versatile tools for interpretation.
So, where do Kolmogorov-Arnold Networks (KANs) fit in this framework? KANs represent a novel approach, where the model's architecture inherently supports interpretability. Their goal is to transition from black box models to white box models. While KANs have not yet fully achieved this transition, and it would be premature to declare them as entirely white box models, they are currently the closest approximation we have to such a model.
What Is the Kolmogorov-Arnold Theorem
Kolmogorov-Arnold Networks (KANs) are a special type of neural network inspired in its design by a mathematical theorem known as the Kolmogorov-Arnold representation theorem. This theorem states the following:
" If f is a multivariate continuous function on a bounded domain, then f can be written as a finite composition of continuous functions of a single variable and the binary operation of addition."
The definition above is quite complex, so let us simplify it. The theorem essentially means that a complicated function involving many variables can be decomposed into a series of simpler functions, each with just one variable.
Let us compare the architecture of a Multi-Layer Perceptron (MLP) to a Kolmogorov-Arnold Network (KAN) model. This is done to understand how this works in practice and why it represents traditional neural network approaches, where weights are used.
Article continues below
Want to learn more? Check out some of our courses:
What is the difference between Multi-Layer Perceptrons and Kolmogorov-Arnold Networks
The entire concept of using neural networks is based on the Universal Approximation Theorem that states the following:
"A neural network with at least one hidden layer of a sufficient number of neurons, and a non-linear activation function can approximate any continuous function to an arbitrary level of accuracy."
In essence, nearly every problem or real-world process can be described by a mathematical function. However, because of the complexity of these processes, the corresponding functions are also quite complex. In theory, one could identify an ideal mathematical function that perfectly captures the desired behavior. However, in practice, accomplishing this is often not feasible.
For example, a mathematical function could theoretically exist that perfectly predicts the price based on features such as size (in square feet), number of bedrooms, number of bathrooms, and age. However, finding this exact function in practice is nearly impossible. Instead, we train a neural network to approximate this function. In other words, we train our network to learn a function that closely resembles, but is not identical to, the ideal function that describes the relationships between these variables.
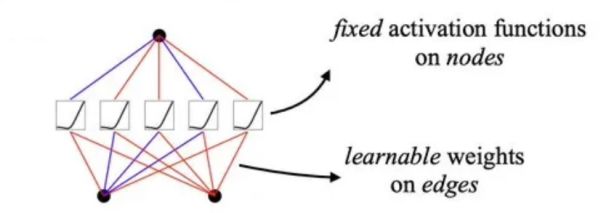
A conventional neural network, specifically a Multi-Layer Perceptron (MLP), accomplishes this through layers of neurons. Each neuron (also known as nodes) is a small processing unit that takes certain input values (like the number of bedrooms, number of bathrooms, etc.) and multiplies them by weights. It then sums these weighted inputs and passes the result through a non-linear activation function, producing an output value.
Each layer contains multiple neurons, all receiving the same input values but using different weights. Once every neuron in a layer generates an output, these outputs become the inputs for the next layer. This process repeats through the successive layers until the final layer, where the network produces a prediction. According to that prediction, the weights of the network are updated to ensure a better final prediction for next time. Moreover, the non-linear activation functions are fixed and remain the same during training.
Multi-Layer Perceptron (https://arxiv.org/abs/2406.13155)
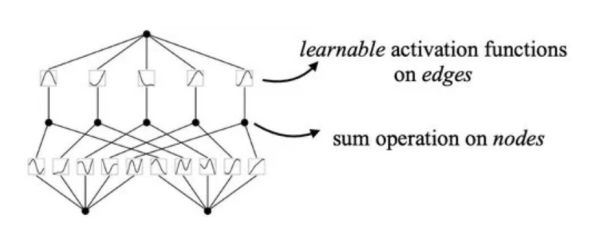
Kolmogorov-Arnold Networks marks a radical shift from the conventional neural network paradigm by redefining how networks learn through changes to activation functions. In standard Multi-Layer Perceptrons (MLPs), complex multivariate functions are approximated using fixed activation functions across multiple layers of nodes.
The KAN theorem states that any continuous multivariate function can be expressed as a finite combination of simpler, one-variable functions In other words, the way that a neural network approaches the problem of approximation can be modified. Instead of approximating a function with a series of linear functions and fixed activation functions, we aim to use multiple smaller functions. In practice, this means that the activation functions are no longer fixed in a KAN model.
Instead, they are something that the model optimizes during training. Linear weights do not exist at all, and we replace them with activation functions that are trainable and depend on a single variable. They are the multiple, smaller univariate functions mentioned in the KAN theorem.
Kolmogorov-Arnold Network (https://arxiv.org/abs/2406.13155)
How do B-Splines function as the weights of the Kolmogorov-Arnold Networks
The fixed non-linear activation functions used in conventional neural networks are well-known to most people in the field of AI. These functions represent an important hyperparameter in our neural networks. However, once the activation functions for particular layers are selected, they remain unchanged during training. Therefore, there is not much else to manage regarding them.
In Kolmogorov-Arnold Networks (KANs), however, we need to train the activation functions. This means we must modify them during training based on the outcomes of our models. In conventional networks, we have fixed linear weights that are initialized randomly. During backpropagation, we use gradient descent to optimize these weights based on the network's output. We calculate the gradient of the weight and adjust the weight value in the direction opposite to the gradient by a certain amount. This process works because the weights are fixed values that we can initialize randomly.
- Human vs. AI: Why AI (Probably) Won't Take Your Job
- What Are 8 Critical Steps in the AI Project Life Cycle?
But in KANs, where actual functions need to be trained, the process is more complex. How do we initialize these functions? How can we ensure they are modified sufficiently during training so that the overall model output changes effectively?
This is where splines, more precisely B-Splines, come into play. Splines are a mathematical concept used to create smooth curves through a set of points. They are especially useful in fields like computer graphics, data fitting, and numerical analysis. The general idea is to piece together several polynomial functions in a manner that they join smoothly at certain points called knots.
B-splines, or Basis splines, are a special type of spline function characterized by their local control property. To simplify, changing the position of a single knot affects only a limited portion of the entire spline. This makes it easier to manipulate and refine specific sections of the curve without altering the entire shape.
Spline (https://rohangautam.github.io/blog/b_spline_intro/#splines)
By adjusting its shape, the spline can model complex relationships. When we first create a spline with a set number of polynomials, it won't necessarily pass through the knots, or even be close to them. However, through training, it can be shaped to better fit the data. This is where B-Splines show their special property: their ability to refine specific sections of the spline without heavily moving the entire spline.
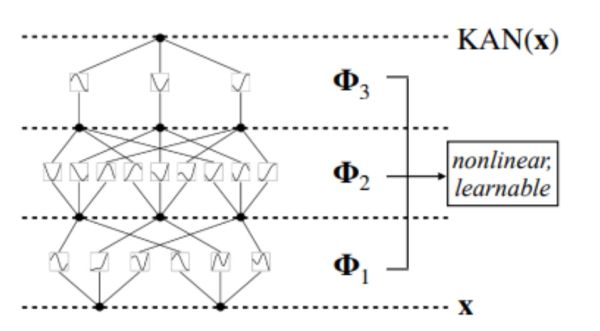
Through the process of adapting its shape, the spline "learns" the subtle patterns that exist in our data. Therefore, these splines represent the learnable activation functions in our KANs. Similar to how we have multiple weights multiplying the same input and going into different neurons, here we will have multiple splines connected to the same input. Each spline will be trained separately from the other. We will also have multiple layers of these, once again similar to what you can usually find in a standard MLP.
Multi-Layer KAN (https://arxiv.org/abs/2406.13155)
What Is the Interpretability of KANs
One of the main advantages of KANs is their interpretability, as was mentioned at the beginning. The main source of interpretability is the fact that, at the end of the training, we have the set of functions that leads from the inputs to the predicted output. In other words, we have our splines. Furthermore, the authors of the paper that introduces KANs offer two additional methods of making the model even more interpretable:
- pruning
- symbolification
Pruning involves removing certain "branches" of our network. More precisely, L1 regularization is applied to the trained activation functions. By evaluating the L1 norms of each function and comparing them to a threshold, we can identify neurons and edges with norms below the threshold as non-essential. These components are then removed from the network, reducing its size and making it easier to analyze and interpret.
Symbolification on the other hand involves replacing the learned univariate functions with known symbolic expressions. Primarily, we analyze the learned functions and propose symbolic candidates based on their shapes and behaviors (e.g., sin, exp). Then we use methods such as the grid search method to adjust the parameters of the symbolic functions. This way they can closely approximate the learned functions.
For example, let us say that one of the learned functions resembles in shape the sine function. What we can do is try to approximate the learned functions with a candidate symbolic expression such as:
f(x)=A sin(Bx+C)Then we use a grid search method, or any other search method, to find the best possible values for A, B, and C. This ensures that this new variant of the sine function can efficiently replace the learned function in our network. For instance, we might determine that the best-fit parameters are A=1.0, B=1.5, and C=0.0. This will allow us to replace the function defined with the spline in our network with:
f(x)=sin(1.5x)
This approach further simplifies the network by replacing arbitrary spline-defined functions with well-known and widely analyzed variants of common mathematical functions.
What Are Other Advantages of KANs
The benefits of KANs extend beyond their enhanced interpretability. Other notable advantages over traditional networks include:
- efficiency
- scalability
- accuracy
The efficiency of KANs is a direct byproduct of how they work. By breaking down complex functions into simpler components, the training process is accelerated and computational costs are reduced. Additionally, KANs are particularly adept at handling high-dimensional data. This is especially advantageous in domains such as image and speech recognition where data dimensionality is vast. Finally, the precise decomposition and recombination of functions enable KANs to potentially achieve higher accuracy compared to traditional models.
However, it should be noted that KANs are still relatively new and have not been extensively tested in industry applications. So far, their advantages over conventional networks have mainly been demonstrated on specific benchmark datasets. Comprehensive industry testing will be necessary to confirm that KANs consistently outperform traditional models in these aspects.
Kolmogorov-Arnold Networks (KANs) have the potential to signify a groundbreaking shift in the landscape of deep learning. Their unique approach to function decomposition and interpretability suggests a potential paradigm shift away from traditional neural networks. KANs have demonstrated significant promise in terms of efficiency, scalability, and accuracy on benchmark datasets. However, their true potential is yet to be fully explored and validated through extensive industry application. As research and experimentation continue, KANs could unlock new levels of performance and understanding in artificial intelligence, heralding a new era in the field of deep learning.