Table of Contents
The brilliance of ChatGPT is its simplicity – even people who are not experts in AI can use it. Trying to understand the inner workings of ChatGPT may seem daunting, but I want to help demystify it step-by-step. In this article, I’ll delve into the Transformer model that ChatGPT is based on. First, I’ll explore why it was developed. Then I’ll explain how one of its two main components, the Encoder block, works.
What Are the Main Concepts Behind Language Models?
Computers can’t understand text, they only understand numbers, and this makes it difficult for computers to understand human language. To make things more complicated, language is sequential and words depend on one another to make sense, so to get your computer to understand language you also need to represent the connections between words to convey the meaning of a sentence. To help computers understand human language you must solve two main problems:
- How can you represent text data in a way a computer can understand?
- How can you explain the idea of a "sequence" of interconnected data?
Most solutions to the first problem are variants of the same idea: “If computers can't understand text, let's represent words through numbers.” These numeric representations are called word embeddings. There are many ways of converting text data into word embeddings, but the goal is always the same: you want to capture the essence of a word by representing it numerically.
In practice, you use vectors to represent words numerically because that way you can use similar vectors for words with similar meanings, so the word doesn't lose its meaning. For example, you can use a similar vector for "large" and "big." Throughout the years, data scientists have found ways to include more information in word embeddings – like information about the position of a word in a sentence, which I’ll tackle later in this article – but the general idea of how you represent text data as vectors hasn't changed much.
The second problem is much harder to solve. Because of how human language works, you can combine words in infinite ways when forming sentences. This makes it impossible to create a set of rules that a computer can follow in every possible situation. Many solutions have been proposed to solve this problem, but the most successful ones are Recurrent Neural Networks and Transformer models.
What Are Recurrent Neural Networks?
Recurrent Neural Networks and their variants used to be at the forefront of Natural Language Processing (NLP). In particular, variants of the architecture called Long Short-Term Memory (LSTM) models were very good at modeling connections between words represented as word embeddings (especially more advanced variants of LSTM models such as Bidirectional LSTM models). LSTMs and their variants dominated the NLP landscape. They were the model to use when solving any NLP problem.
Explaining how LSTMs work could be a whole article on its own. To put it simply, these networks use “cells” that can store both long-term and short-term memory. Each cell takes in three inputs:
- A word in the form of a word vector.
- A hidden-state vector that represents the short-term memory of the cell.
- A cell-state vector that represents the long-term memory of the cell.
Multiple complex calculations occur in each cell and you get two outputs: a new hidden-state vector and a new cell-state vector. The new hidden-state vector is used both as input for the next cell and as the result of processing a word in that cell. On the other hand, you use the cell-state vector as one of the inputs for a following cell.
This is a gross oversimplification of the whole process, but it demonstrates one main design philosophy behind any LSTM which is, in order to calculate the output of a cell, you need to first calculate the hidden-state vector and the cell-state vector of the previous cell. This leads to the two main drawbacks of LSTMs.
The first drawback is that the length of a sequence you can process is limited. While the hidden-state vector and the cell-state vector simulate short-term and long-term memory nicely when you work with shorter text sequences, if you try to input a longer sequence (for example, a paragraph of a thousand words), the information it carries gets diluted.
The second drawback is that you can't parallelize the training process. In Deep Learning, you leverage the fact that you can’t parallelize the training process because it allows you to speed up model training. Speed is necessary if you want to build huge models that use a lot of parameters, because otherwise training huge models will take an extremely long time. Because you need to calculate the outputs of the previous cell before moving on to the next cell, LSTMs are limited and training them is extremely slow compared to other architectures.
Article continues below
Want to learn more? Check out some of our courses:
What Are Transformer Models?
Ashish Vaswani and his colleagues first introduced the Transformer architecture in a paper called "Attention Is All You Need" in 2017. Their goal was to solve the issues that plagued LSTM models, especially in machine translation. While the original model was designed for machine translation, its variants (such as the GPT model) found their place in various applications. To understand how the Transformer model works, I’ll look at how it translates a sentence from English to French.
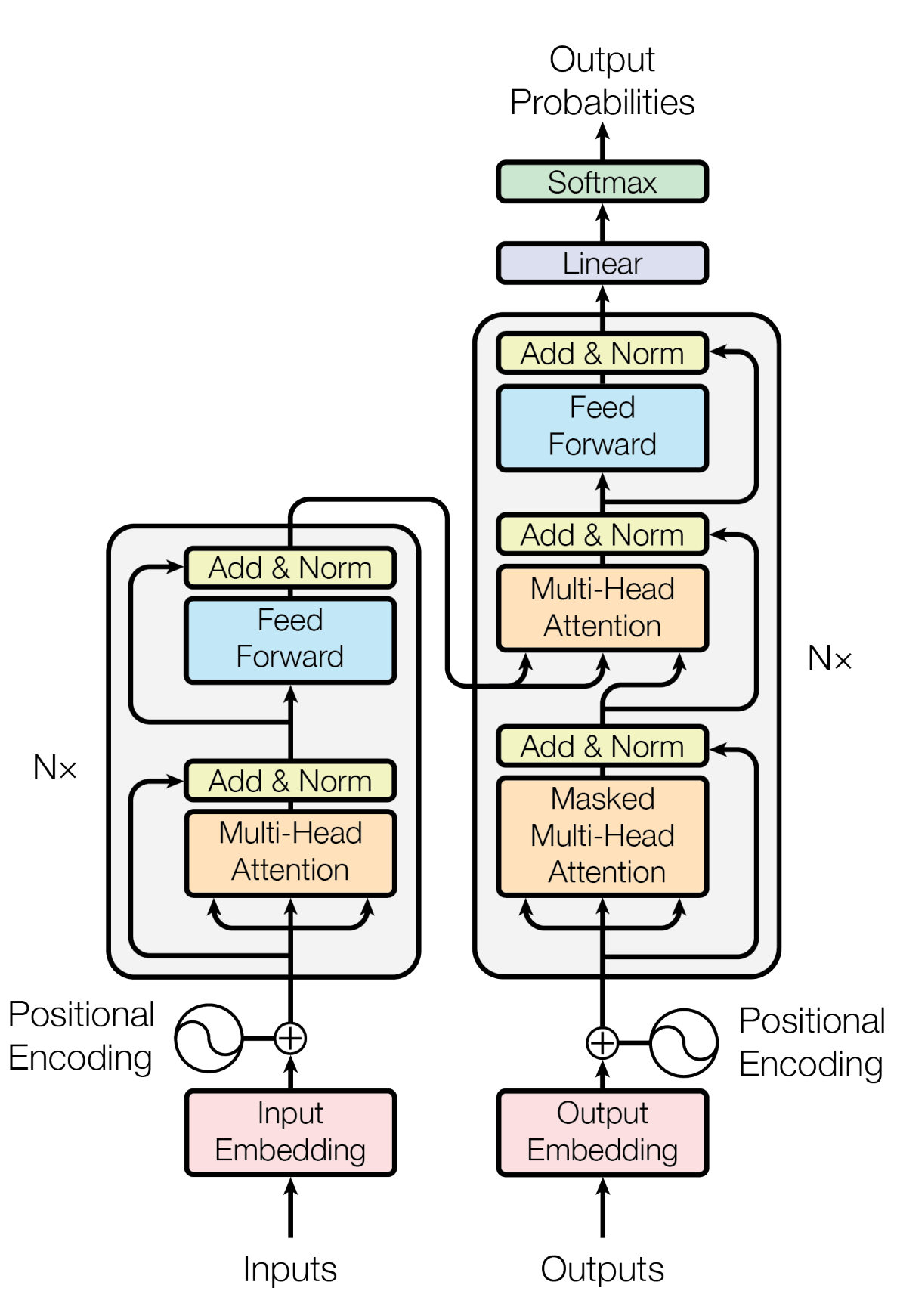
To understand how a model translates text, you must first understand its architecture. As you can see below, the architecture of a Transformer model is a lot more complex than that of an LSTM model:
Architecture of the Transformer model.
Image source: Vaswani, A., et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
The Transformer model can be separated into two main parts: the Encoder and Decoder blocks, each consisting of multiple sub-parts. In the rest of this article, I’ll focus on the Encoder block. In the next article, I’ll delve into the details of the Decoder block.
How Does the Encoder Block Work?
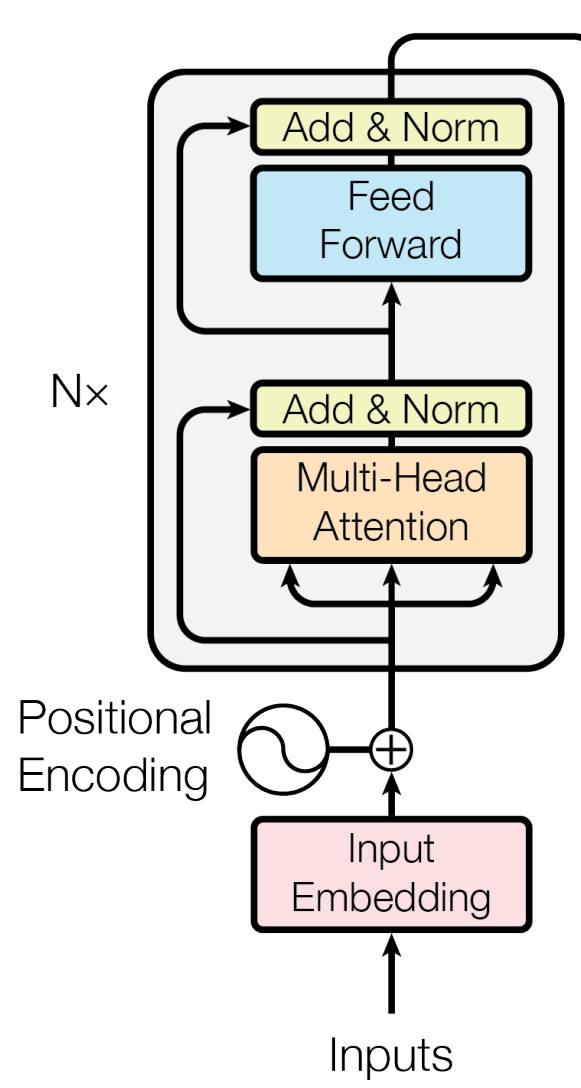
Image source: Vaswani, A., et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
The encoder block of a Transformer model consists of the following parts:
- A Positional Encoder
- Multi-Head Self-Attention
- A Feed-Forward Network
I’ll go through these one-by-one to make sure you understand what they do.
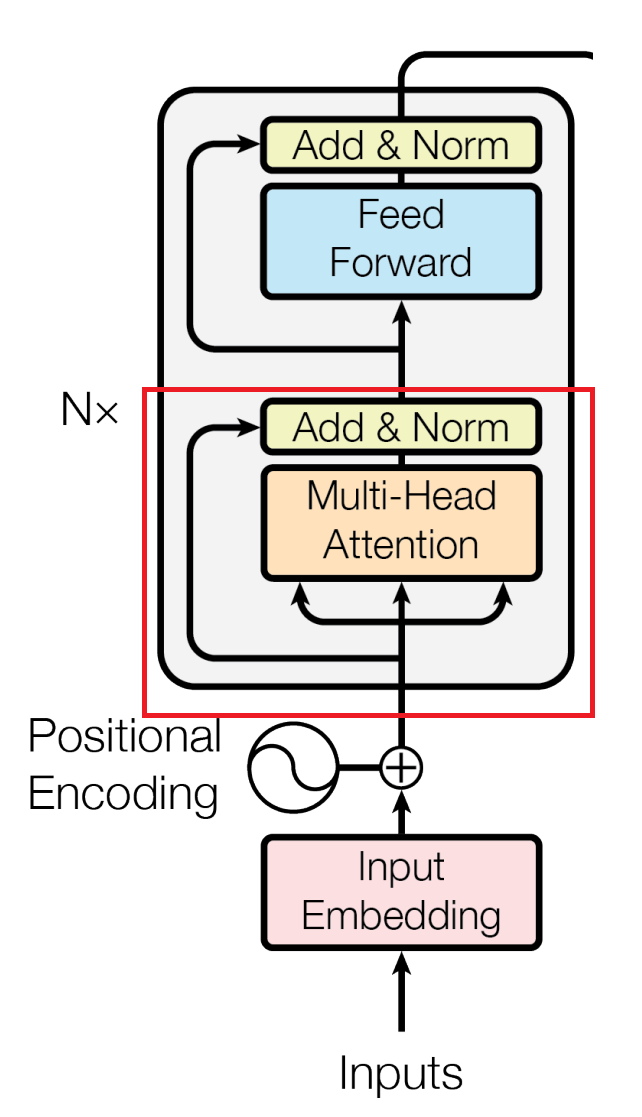
What is a Positional Encoder?
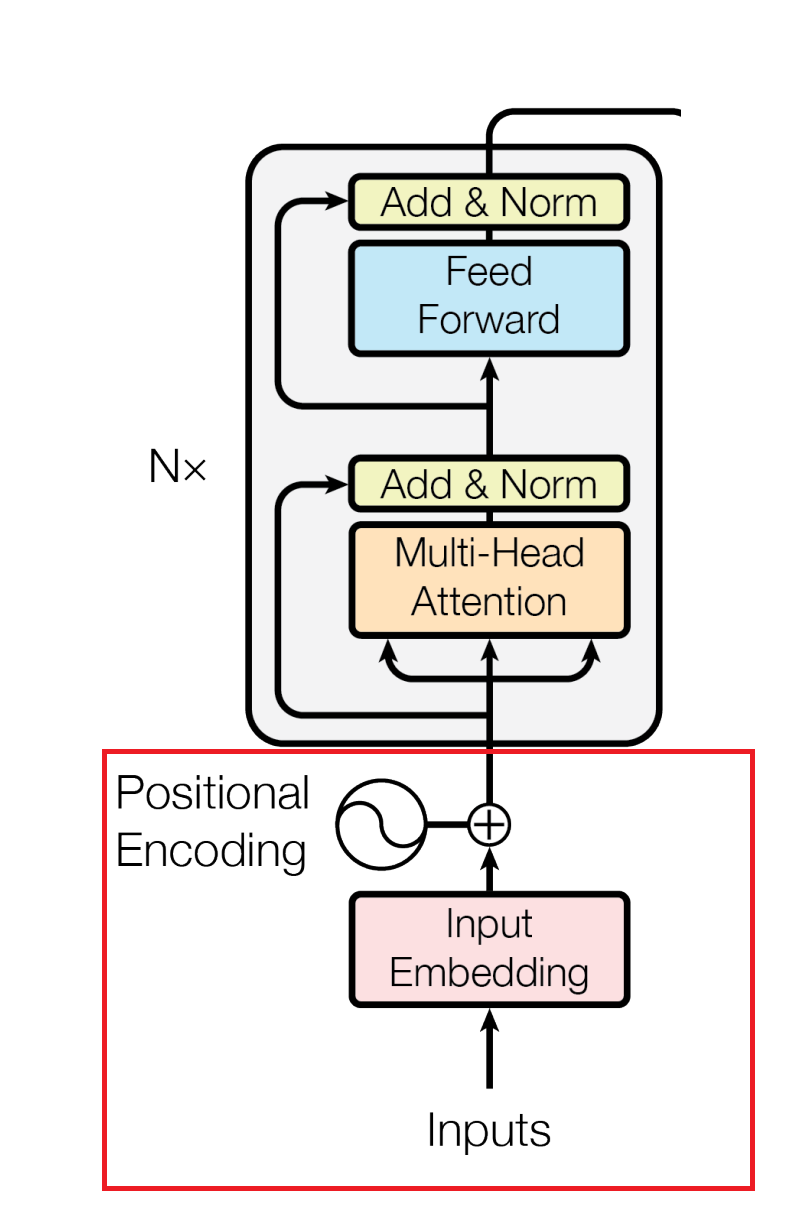
Image source: Vaswani, A., et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
As I mentioned previously, a word's position in a sentence plays a big role in determining its meaning. Recurrent Neural Networks preserve the order of words by taking in one word at a time in the order they are in the sentence. However, as mentioned previously, you can feed Transformer models multiple words simultaneously. You can even feed whole paragraphs of text to your model. To ensure that your model still understands a word's position in a sentence, you need to perform an operation known as Positional Encoding.
Positional Encoding ensures that your model knows the order of words in a sentence, even when you input multiple words simultaneously. To positionally encode words, you take your input word embeddings (the vectors representing words) and add values that define their position in the sentence. To be more precise, you create “positional vectors” by solving a mathematical function. These positional vectors don't represent a specific word but instead a position in the sentence.
Let's say you’re working with the sentence "The dog barked at the cat." In this example, I will use 4-dimensional word vectors to represent each word. In reality, word vectors can have dimensions in the range of hundreds, but I’ll simplify the math behind some processes for clarity.
For example, let's say that these are the example starting word vectors:
- The [0.1, 0.2, 0.3, 0.4]
- dog [0.5, 0.6, 0.7, 0.8]
- barked [0.9, 1.0, 1.1, 1.2]
- at [1.3, 1.4, 1.5, 1.6]
- the [1.7, 1.8, 1.9, 2.0]
- cat [1.7, 1.78, 1.89, 2.0]
Next, I’ll calculate positional vectors using a mathematical function. These positional vectors represent the position of each word in the sentence. Remember, I’m using 4-dimensional vectors here, so they will look like this:
- Position 1: [0.01, 0.02, 0.03, 0.04]
- Position 2: [0.05, 0.06, 0.07, 0.08]
- Position 3: [0.09, 0.10, 0.11, 0.12]
- Position 4: [0.13, 0.14, 0.15, 0.16]
- Position 5: [0.17, 0.18, 0.19, 0.20]
- Position 6: [0.21, 0.22, 0.23, 0.24]
To get the final vectors for my words, I’ll sum up each word vector with the corresponding positional vector:
- The (position 1): [0.1+0.01, 0.2+0.02, 0.3+0.03, 0.4+0.04] = [0.11, 0.22, 0.33, 0.44]
- dog (position 2): [0.5+0.05, 0.6+0.06, 0.7+0.07, 0.8+0.08] = [0.55, 0.66, 0.77, 0.88]
- barked (position 3): [0.9+0.09, 1.0+0.10, 1.1+0.11, 1.2+0.12] = [0.99, 1.1, 1.21, 1.32]
- at (position 4): [1.3+0.13, 1.4+0.14, 1.5+0.15, 1.6+0.16] = [1.43, 1.54, 1.65, 1.76]
- the (position 5): [1.7+0.17, 1.8+0.18, 1.9+0.19, 2.0+0.20] = [1.87, 1.98, 2.09, 2.20]
- cat (position 6): [1.7+0.21, 1.78+0.22, 1.89+0.23, 2.0+0.24] = [1.91, 2.00, 2.12, 2.24]
Because the positional vectors that I summed up with my original word vectors are all created using the same mathematical function, my model can reliably determine the position of each word in a sentence. So now that I have the word vectors with positional encodings, I can proceed to the Multi-Head Self-Attention mechanism.
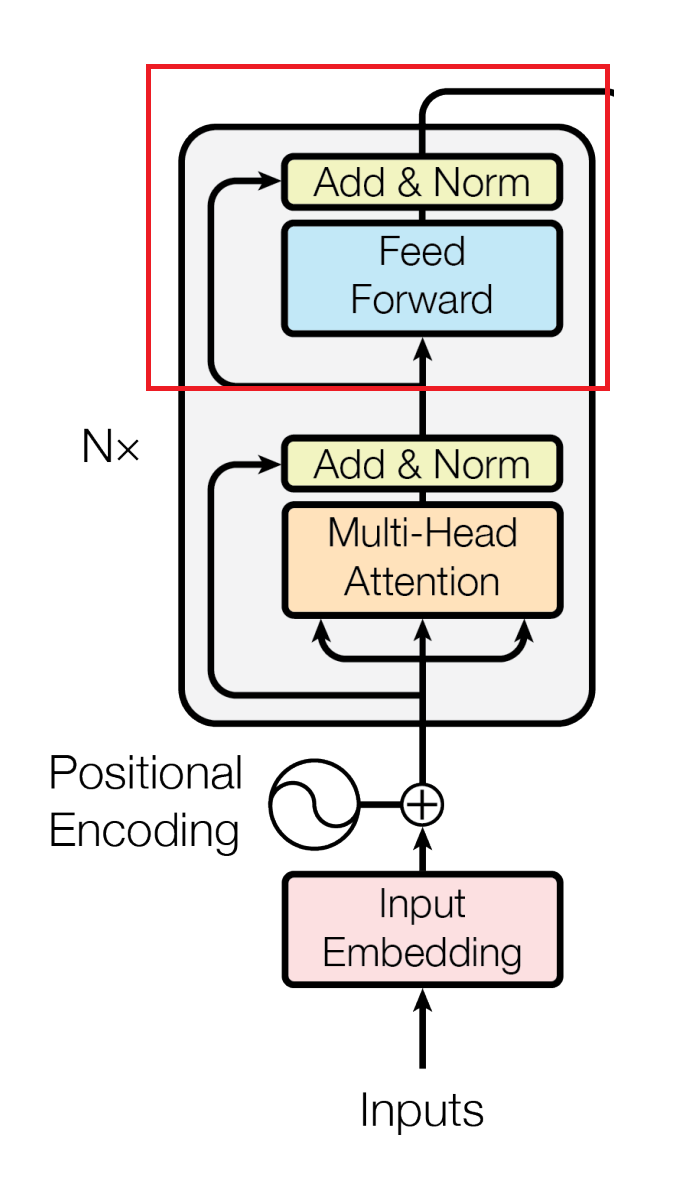
What is Multi-Head Self-Attention?
The Multi-Head Self-Attention mechanism in the Transformer architecture.
Image source: Vaswani, A., et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
I already talked about how attention works in a previous article, but let's now take a look at how the Multi-Head Self-Attention mechanism operates in the Transformer architecture. This part of the Encoder block is vital because it can capture and learn relationships between words even if they are far apart in a text.
In the Multi-Head Self-Attention mechanism, the model determines the importance of each word relative to a specific word by calculating the attention scores between every pair of words in the sentence. For example, consider the word “barked” in the sentence “The dog barked at the cat.” I want to find out how important each word in the sentence is to the word “barked.” To get that information, the model will:
- Calculate attention scores based on the positionally Encoded vectors I created earlier.
- Normalize the attention scores using a Softmax function, which essentially converts them into probabilities indicating the relative importance of each word in the sentence to the word “barked.”
- Compute a weighted sum of the word vectors using the normalized attention scores.
I repeat this process multiple times for each word in the sentence, once for each head in the Encoder block (hence the name Multi-Head Self-Attention). The outputs from each attention head are linked in a series, resulting in a final output vector for each word in the sentence.
The exact process of calculating these attention vectors is very complex, so I won't go into it in detail here. For my purposes, let's say that these are the approximate values of the vectors that I end up with:
- The: [0.28, 0.61, 0.76, 0.45]
- dog: [0.66, 0.73, 0.82, 0.91]
- barked: [0.92, 1.15, 1.28, 1.31]
- at: [1.49, 1.56, 1.68, 1.72]
- the: [1.95, 2.05, 2.12, 2.18]
- cat: [2.01, 2.07, 2.15, 2.23]
Now I can send these vectors to the next part of the Encoder block, the Feed-Forward Network.
What is the Feed-Forward Network?
The Feed-Forward Network in the Transformer architecture.
Image source: Vaswani, A., et al. "Attention is all you need." Advances in neural information processing systems 30 (2017).
After the Multi-Head Self-Attention mechanism, the output vectors for each word in the sentence pass through two additional components in the Encoder block: layer normalization and the Feed-Forward Network.
Layer normalization is a preprocessing step your data goes through before passing it into the Feed-Forward Network. It helps improve the Transformer model's training by adjusting the output vectors of the Multi-Head Self-Attention mechanism so that they have similar ranges of values. This allows the model to learn more effectively because it prevents extreme values from dominating the learning process or causing instability in training.
The Feed-Forward Network further processes the normalized vectors. The network receives each output vector separately and adjusts it so that the model can better understand the context and relationships between different words in a text. The network combines and transforms the input value through its two linear layers and the Rectified Linear Unit (ReLU) activation function, which is the default activation function used in Feed-Forward Networks nowadays due to its simplicity and effectiveness. By feeding the words to the network, you get more expressive and meaningful representations of them.
Let's assume that I obtained the following new vectors for each word in my example sentence:
- The: [0.48, 0.92, 1.03, 0.65]
- dog: [1.01, 1.10, 1.21, 1.32]
- barked: [1.35, 1.57, 1.68, 1.73]
- at: [1.86, 1.93, 2.04, 2.08]
- the: [2.35, 2.43, 2.50, 2.56]
- cat: [2.45, 2.51, 2.59, 2.68]
Remember that the word vectors I’m using here are vastly simplified to illustrate how they change as they pass through the model. In reality, both layers of the Encoder block (and the Decoder block, which I’ll cover in the next article in this series) are defined by a large number of parameters. The actual Transformer model uses more than 65 million parameters!
I hope you now better understand why the Transformer model was created and how its Encoder block transforms sentences into vectors containing information, not only about the words themselves, but also about their relationship to other words in the sentence. In the next article in this series, I will cover how the Decoder block of the Transformers architecture works and explain the similarities and differences between a standard Transformer architecture and the GPT architecture.
- Read next: Intro to Transformers: The Decoder Block >>